The Figure of Merit in Time (FMT) is a statistical coefficient of the time analysis.
The FMT is calculated at a fixed location ![]() , for a time series of data. It is defined as:
, for a time series of data. It is defined as:
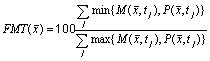
Analogous to the FMS, the FMT evaluates for a fixed location the overlapping concentration histogram, normalised to the time series of the maximum concentration, measured or predicted, at each time interval. As the FMS, the FMT is expressed in percent.
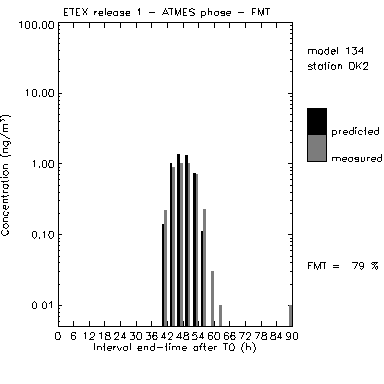
An example of FMT analysis is shown in Figure 7.
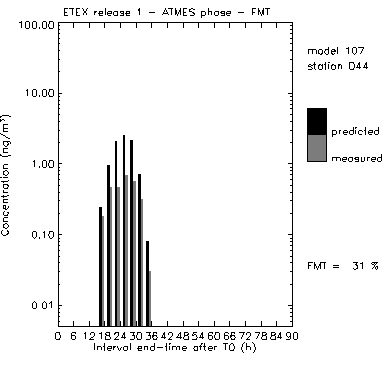
A temporal shift of the time series can reduce significantly the FMT, even if predicted duration and concentration values are in good agreement with measurements. Also, a difference between predicted and modelled values can give a small FMT, even if time of arrival and duration are correctly predicted (Figure 8).
To understand the sensitivity of the FMT coefficient to the difference between predictions and measurements, the FMT of measurements against alterations of them were considered.
In particular, the values of concentration measured at samplers D5 and NL5 were multiplied by a factor (2 or 5) and shifted in time (3 and 6 hours).
The results of this sensitivity study for the two stations D5 and NL5, which respectively have, a regular and an irregular time evolution are shown in Figure 9.
It can be observed that an irregular time series is more sensitive to these differences than a regular one. The results of this sensitivity analysis can also give indications on the interpretation of FMT values obtained for the models. The only shift of 3 hours (one time interval) of the same regular (D5) data set reduces the FMT from 100% to 57%. The factor 2 multiplication obviously halves by 2 the FMT. Thus, a model having a 50% FMT compared to measurements must be considered as a good performer.
 |
|
Figure 7. Time series and FMT calculation at station DK2 for one of the ATMES II models. Good agreement in times and concentration values.
|
 |
|
Figure 8. Time series at station D44 for one of the ATMES II models. Good agreement in times but not in concentration values causes a small FMT.
|
 |
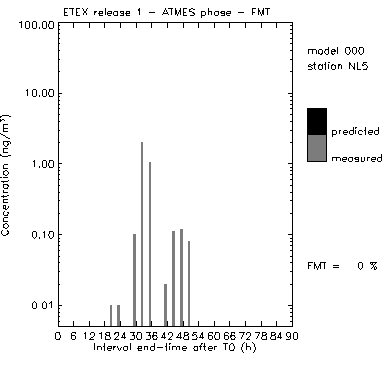 |
| Figure 9. Measured concentration time series in D5 (regular trend) and NL5 (irregular trend). |
Table 4. FMT (%) of measurements versus modified measurements in D5, which has a regular time evolution, and in NL5, which has an irregular time evolution. Sensitivity of FMT to a shifting of 1 or 2 time intervals (correspondent to 3 or 6 hours) and to a multiplication by a factor 2 and 5.
|
D5 |
Shifting time(h) |
NL5 |
Shifting time(h) |
|||||||
|
0 |
3 |
6 |
0 |
3 |
6 |
|||||
|
multiplication factor |
1 |
100 |
57 |
33 |
multiplication factor |
1 |
100 |
24 |
3 |
|
|
2 |
50 |
45 |
28 |
2 |
50 |
29 |
3 |
|||
|
5 |
20 |
20 |
18 |
5 |
20 |
13 |
2 |
|||